Today i am solving this important question of triangles its very hard to solve .Find this important question of ncert class 9th of chapter triangles .Sir please help me to find out the easiest and simplest solution of question 5 of exercise 7.1, give me the best solution of this question. Line l is the bisector of an angle A and B is any point on l. BP and BQ are perpendiculars from B to the arms of A (see Fig. 7.20). Show that: (i) ΔAPB ΔAQB (ii) BP = BQ or B is equidistant from the arms of A.
SonuNewbie
Line l is the bisector of an angle A and B is any point on l. BP and BQ are perpendiculars from B to the arms of A (see Fig. 7.20). Show that: (i) ΔAPB ΔAQB (ii) BP = BQ or B is equidistant from the arms of A. Q.5
Share



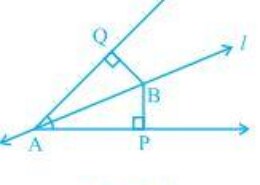

It is given that the line “l” is the bisector of angle A and the line segments BP and BQ are perpendiculars drawn from l.
(i) ΔAPB and ΔAQB are similar by AAS congruency because:
P = Q (They are the two right angles)
AB = AB (It is the common arm)
BAP = BAQ (As line l is the bisector of angle A)
So, ΔAPB ΔAQB.
(ii) By the rule of CPCT, BP = BQ. So, it can be said the point B is equidistant from the arms of A.