Find this important question of ncert class 9th of chapter triangles .Sir please help me to find out the easiest and simplest solution of question 8(2),(3),(4) of exercise 7.1, give me the best solution of this question.. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:(ii) DBC is a right angle. (iii) ΔDBC ΔACB (iv) CM = ½ AB
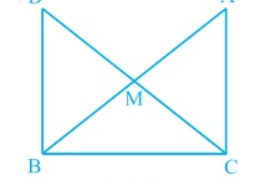
(ii) ACM = BDM (by CPCT)
∴ AC BD as alternate interior angles are equal.
Now, ACB +DBC = 180° (Since they are co-interiors angles)
⇒ 90° +B = 180°
∴ DBC = 90°
(iii) In ΔDBC and ΔACB,
BC = CB (Common side)
ACB = DBC (They are right angles)
DB = AC (by CPCT)
So, ΔDBC ΔACB by SAS congruency.
(iv) DC = AB (Since ΔDBC ΔACB)
⇒ DM = CM = AM = BM (Since M the is mid-point)
So, DM + CM = BM+AM
Hence, CM + CM = AB
⇒ CM = (½) AB
(ii) ACM = BDM (by CPCT)
∴ AC BD as alternate interior angles are equal.
Now, ACB +DBC = 180° (Since they are co-interiors angles)
⇒ 90° +B = 180°
∴ DBC = 90°
(iii) In ΔDBC and ΔACB,
BC = CB (Common side)
ACB = DBC (They are right angles)
DB = AC (by CPCT)
So, ΔDBC ΔACB by SAS congruency.
(iv) DC = AB (Since ΔDBC ΔACB)
⇒ DM = CM = AM = BM (Since M the is mid-point)
So, DM + CM = BM+AM
Hence, CM + CM = AB
⇒ CM = (½) AB