What is the ncert class 9th question of chapter triangles of exercise 7.1 question number 1. Please give me the simplest and easiest solution of this question , also give me the best solution of this question. In quadrilateral ACBD, AC = AD and AB bisect A (see Fig. 7.16). Show that ΔABC ΔABD. What can you say about BC and BD?
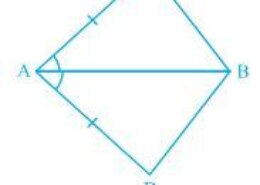
Solution:
It is given that AC and AD are equal i.e. AC = AD and the line segment AB bisects A.
We will have to now prove that the two triangles ABC and ABD are similar i.e. ΔABC ΔABD
Proof:
Consider the triangles ΔABC and ΔABD,
(i) AC = AD (It is given in the question)
(ii) AB = AB (Common)
(iii) CAB = DAB (Since AB is the bisector of angle A)
So, by SAS congruency criterion, ΔABC ΔABD.
For the 2nd part of the question, BC and BD are of equal lengths by the rule of C.P.C.T.