This is very important question of ncert class 9th of chapter triangles. How I solve the best solution of exercise 7.1 question number 6. Please help me to solve this in a easy and best way ad give me the simple method of this question. In Fig. 7.21, AC = AE, AB = AD and BAD = EAC. Show that BC = DE.
Share



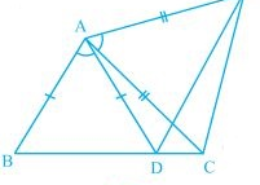

Solution:
It is given in the question that AB = AD, AC = AE, and ∠BAD = ∠EAC
To prove:
The line segment BC and DE are similar i.e. BC = DE
Proof:
We know that BAD = EAC
Now, by adding DAC on both sides we get,
BAD + DAC = EAC +DAC
This implies, BAC = EAD
Now, ΔABC and ΔADE are similar by SAS congruency since:
(i) AC = AE (As given in the question)
(ii) BAC = EAD
(iii) AB = AD (It is also given in the question)
∴ Triangles ABC and ADE are similar i.e. ΔABC ΔADE.
So, by the rule of CPCT, it can be said that BC = DE.