Sir please help me to solve the ncert class 9th solution of chapter triangles.How I solve this question of exercise 7.1 question number 2. Find the simplest and easiest solution of this question , also give me the best solution of this question .ABCD is a quadrilateral in which AD = BC and DAB = CBA (see Fig. 7.17). Prove that (i) ΔABD ΔBAC (ii) BD = AC (iii) ABD = BAC.
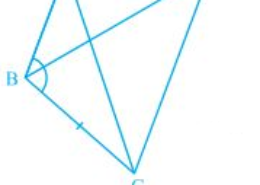
The given parameters from the questions are DAB = CBA and AD = BC.
(i) ΔABD and ΔBAC are similar by SAS congruency as
AB = BA (It is the common arm)
DAB = CBA and AD = BC (These are given in the question)
So, triangles ABD and BAC are similar i.e. ΔABD ΔBAC. (Hence proved).
(ii) It is now known that ΔABD ΔBAC so,
BD = AC (by the rule of CPCT).
(iii) Since ΔABD ΔBAC so,
Angles ABD = BAC (by the rule of CPCT).