Sir please help me to solve the ncert class 9th solution of chapter triangles.How I solve this question of exercise 7.1 question number 7. Find the simplest and easiest solution of this question , also give me the best solution of this question.
SonuNewbie
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that BAD = ABE and EPA = DPB (see Fig. 7.22). Show that (i) ΔDAP ΔEBP (ii) AD = BE . Q.7
Share



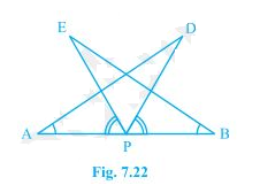

In the question, it is given that P is the mid-point of line segment AB. Also, BAD = ABE and EPA = DPB
(i) It is given that EPA = DPB
Now, add DPE on both sides,
EPA +DPE = DPB+DPE
This implies that angles DPA and EPB are equal i.e. DPA = EPB
Now, consider the triangles DAP and EBP.
DPA = EPB
AP = BP (Since P is the mid-point of the line segment AB)
BAD = ABE (As given in the question)
So, by ASA congruency, ΔDAP ΔEBP.
(ii) By the rule of CPCT, AD = BE.