Today i am solving the ncert class 9th question of chapter triangles of exercise 7.3 quesztion number 1(ii). Find the easiest and simplest way to solve this question its very important question of this chapter. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that(ii) ΔABP ΔACP
SonuNewbie
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that(ii) ΔABP ΔACP Q.1(ii)
Share



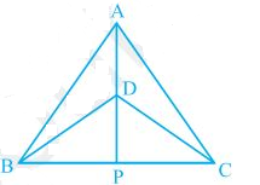

(ii) ΔABP and ΔACP are similar as:
AP = AP (It is the common side)
PAB = PAC (by CPCT since ΔABD ΔACD)
AB = AC (Since ΔABC is isosceles)
So, ΔABP ΔACP by SAS congruency condition.