What is the easiest way for solving the question of class 9th ncert math of exercise 10.5of math of Circles chapter of question no.9 Please help me for the best suggestion of this question Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ ACP = ∠ QCD
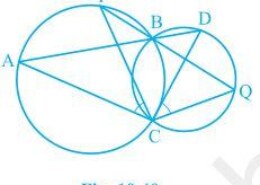
Join the chords AP and DQ.
For chord AP, we know that angles in the same segment are equal.
So, ∠ PBA = ∠ ACP — (i)
Similarly for chord DQ,
∠ DBQ = ∠ QCD — (ii)
It is known that ABD and PBQ are two line segments which are intersecting at B.
At B, the vertically opposite angles will be equal.
∴ ∠ PBA = ∠ DBQ — (iii)
From equation (i), equation (ii) and equation (iii) we get,
∠ ACP = ∠ QCD