How i solve this question of class 10th math of exercise 6.6 of Triangles chapter , Please suggest me the best way to solve this problem because it is very important question also In Figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that : (i) AC2 = AD2 + BC.DM + 2 (BC/2) 2
AnilSinghBoraGuru
In Figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that : (i) AC2 = AD2 + BC.DM + 2 (BC/2) 2 Q.5(1)
Share



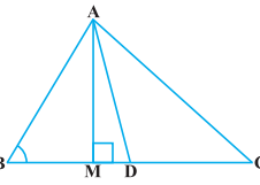

By applying Pythagoras Theorem in ∆AMD, we get,
AM2 + MD2 = AD2 ………………. (i)
Again, by applying Pythagoras Theorem in ∆AMC, we get,
AM2 + MC2 = AC2
AM2 + (MD + DC) 2 = AC2
(AM2 + MD2 ) + DC2 + 2MD.DC = AC2
From equation(i), we get,
AD2 + DC2 + 2MD.DC = AC2
Since, DC=BC/2, thus, we get,
AD2 + (BC/2) 2 + 2MD.(BC/2) 2 = AC2
AD2 + (BC/2) 2 + 2MD × BC = AC2
Hence, proved.