For class 10 Triangles chapter of exercise 6.6 of ncert math, how i solve this chapter because it is an optional exercise and i don’t know how to solve this problem, In Figure, ABC is a triangle in which ∠ ABC < 90° and AD ⊥ BC. Prove that AC2= AB2+ BC2 – 2 BC.BD.
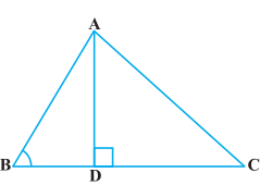
By applying Pythagoras Theorem in ∆ADB, we get,
AB2 = AD2 + DB2
We can write it as;
⇒ AD2 = AB2 − DB2 ……………….. (i)
By applying Pythagoras Theorem in ∆ADC, we get,
AD2 + DC2 = AC2
From equation (i),
AB2 − BD2 + DC2 = AC2
AB2 − BD2 + (BC − BD) 2 = AC2
AC2 = AB2 − BD2 + BC2 + BD2 −2BC × BD
AC2 = AB2 + BC2 − 2BC × BD
Hence, proved.