Yesterday i was doing the question from class 9th ncert book of math of Areas of Parallelograms and Triangles chapter of exercise 9.4 What is the easiest way for solving it because i was not able to do this question please help me for solving this question In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:(iv) ar (BFE) = ar (AFD)
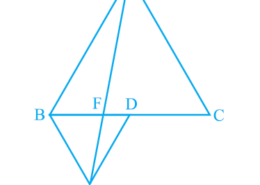
ΔBDE and ΔAED lie on the same base (DE) and are in-between the parallel lines DE and AB.
∴ar (ΔBDE) = ar (ΔAED)
Subtracting ar(ΔFED) from L.H.S and R.H.S,
We get,
∴ar (ΔBDE)−ar (ΔFED) = ar (ΔAED)−ar (ΔFED)
∴ar (ΔBFE) = ar(ΔAFD)
Hence proved