Please give me the best way for solving the problem of class 9th ncert math of Areas of Parallelograms and Triangles chapter of math of class 9th of exercise 9.4 of question no 5(3) what is the tricky way for solving this question In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:(iii) ar (ABC) = 2 ar (BEC)
AnilSinghBoraGuru
In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:(iii) ar (ABC) = 2 ar (BEC) Q.5(3)
Share



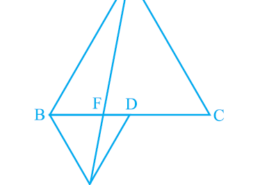

ar(ΔABE) = ar(ΔBEC) [Common base BE and BE || AC]
ar(ΔABF) + ar(ΔBEF) = ar(ΔBEC)
From eqn (i), we get,
ar(ΔABF) + ar(ΔAFD) = ar(ΔBEC)
ar(ΔABD) = ar(ΔBEC)
½ ar(ΔABC) = ar(ΔBEC)
ar(ΔABC) = 2 ar(ΔBEC)
Hence proved