How i solve this question of Triangles chapter of exercise 6.6 of ncert math of question no.8 give me the best way to solve this problem i think it is very important for class 10th In Fig. 6.62, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that: (i) ∆ PAC ~ ∆ PDB (ii) PA . PB = PC . PD.
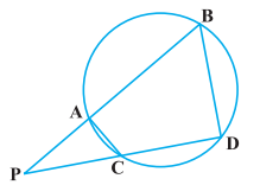
(i) In ∆PAC and ∆PDB,
∠P = ∠P (Common Angles)
As we know, exterior angle of a cyclic quadrilateral is ∠PCA and ∠PBD is opposite interior angle, which are both equal.
∠PAC = ∠PDB
Thus, ∆PAC ∼ ∆PDB(AA similarity criterion)
(ii) We have already proved above,
∆APC ∼ ∆DPB
We know that the corresponding sides of similar triangles are proportional.
Therefore,
AP/DP = PC/PB = CA/BD
AP/DP = PC/PB
∴ AP. PB = PC. DP