Today I am solving the ncert class 9th solution of chapter triangles.Find the best solution of exercise 7.2 question number 2, also find the simplest and easiest solution of this question. Please help me to solve this question. In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC.
SonuNewbie
In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC. Q.2
Share



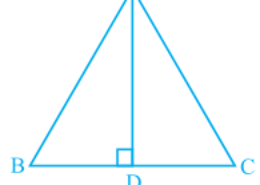

Solution:
It is given that AD is the perpendicular bisector of BC
To prove:
AB = AC
Proof:
In ΔADB and ΔADC,
AD = AD (It is the Common arm)
ADB = ADC
BD = CD (Since AD is the perpendicular bisector)
So, ΔADB ΔADC by SAS congruency criterion.
Thus,
AB = AC (by CPCT)