What is the ncert class 9th question of chapter triangles of exercise 7.1 question number 2. Please give me the simplest and easiest solution of this question , also give me the best solution of this question. its very important question of this chapter please solve this in a easy way.In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC.
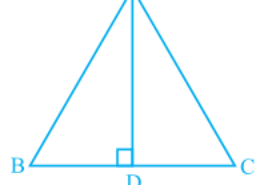
Solution:
It is given that AD is the perpendicular bisector of BC
To prove:
AB = AC
Proof:
In ΔADB and ΔADC,
AD = AD (It is the Common arm)
ADB = ADC
BD = CD (Since AD is the perpendicular bisector)
So, ΔADB ΔADC by SAS congruency criterion.
Thus,
AB = AC (by CPCT)