Find the best solution of this important question of ncert class 9th of chapter triangles . Please help me to solve this question in a easiest and simplest way of exercise 7.2 question number 4 . Find the best and easiest solution of this question.ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that (i) ΔABE ΔACF (ii) AB = AC, i.e., ABC is an isosceles triangle.
SonuNewbie
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that (i) ΔABE ΔACF (ii) AB = AC, i.e., ABC is an isosceles triangle.Q.4
Share



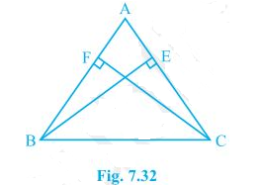

It is given that BE = CF
(i) In ΔABE and ΔACF,
A = A (It is the common angle)
AEB = AFC (They are right angles)
BE = CF (Given in the question)
∴ ΔABE ΔACF by AAS congruency condition.
(ii) AB = AC by CPCT and so, ABC is an isosceles triangle.