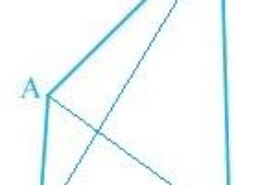
In ΔABD, we see that

AB < AD < BD

So, ADB < ABD — (i) (Since angle opposite to longer side is always larger)

Now, in ΔBCD,

BC < DC < BD

Hence, it can be concluded that

BDC < CBD — (ii)

Now, by adding equation (i) and equation (ii) we get,

ADB + BDC < ABD + CBD

ADC < ABC

B > D

Similarly, In triangle ABC,

ACB < BAC — (iii) (Since the angle opposite to the longer side is always larger)

Now, In ΔADC,

DCA < DAC — (iv)

By adding equation (iii) and equation (iv) we get,

ACB + DCA < BAC+DAC

⇒ BCD < BAD

∴ A > C