Home/ Questions/Q 11539
In Process
Adv
Sonu
  • 0
Newbie
Asked: 2021-08-10T13:04:12+05:30 In:

ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that BCD is a right angle.Q.6

  • 0
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that BCD is a right angle.Q.6

Its very important question of chapter triangles ncert class 9th . Find the best and simplest solution of exercise 7.2 question 6 ,Please help me to solve this question in a best and simplest way.ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that BCD is a right angle.

best math ncert solutionexercise 7.2 ncertncert class 9th solutiontriangles ncert
Share

    1 Answer

    1. Guru

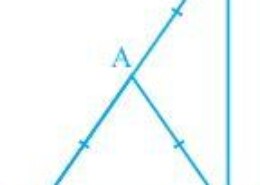
      It is given that AB = AC and AD = AB

      We will have to now prove BCD is a right angle.

      Proof:

      Consider ΔABC,

      AB = AC (It is given in the question)

      Also, ACB = ABC (They are angles opposite to the equal sides and so, they are equal)

      Now, consider ΔACD,

      AD = AB

      Also, ADC = ACD (They are angles opposite to the equal sides and so, they are equal)

      Now,

      In ΔABC,

      CAB + ACB + ABC = 180°

      So, CAB + 2ACB = 180°

      ⇒ CAB = 180° – 2ACB — (i)

      Similarly, in ΔADC,

      CAD = 180° – 2ACD — (ii)

      also,

      CAB + CAD = 180° (BD is a straight line.)

      Adding (i) and (ii) we get,

      CAB + CAD = 180° – 2ACB+180° – 2ACD

      ⇒ 180° = 360° – 2ACB-2ACD

      ⇒ 2(ACB+ACD) = 180°

      ⇒ BCD = 90°

      • 0

    Related Questions

    Adv