Today i am solving the important question of ncert class 9th chapter triangles question of exercise 7.3 question number 1(iv), Find the simplest solution of this question also find the best and easiest solution of this question .. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that(iv) AP is the perpendicular bisector of BC
SonuNewbie
. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that(iv) AP is the perpendicular bisector of BC.Q.1(iv)
Share



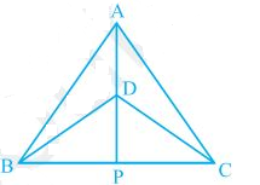

(iv) BPD = CPD (by CPCT as ΔBPD ΔCPD)
and BP = CP — (i)
also,
BPD +CPD = 180° (Since BC is a straight line.)
⇒ 2BPD = 180°
⇒ BPD = 90° —(ii)
Now, from equations (i) and (ii), it can be said that
AP is the perpendicular bisector of BC.