Solution: (i) We have, sin 20o/ cos 70o = sin (90o – 70o)/ cos 70o = cos 70o/ cos70o = 1 [∵ sin (90 – θ) = cos θ] (ii) We have, cos 19o/ sin 71o = cos (90o – 71o)/ sin 71o = sin 71o/ sin 71o = 1 [∵ cos (90 – θ) = sin θ]
Solution:
(i) We have,
sin 20o/ cos 70o = sin (90o – 70o)/ cos 70o = cos 70o/ cos70o = 1 [∵ sin (90 – θ) = cos θ]
(ii) We have,
cos 19o/ sin 71o = cos (90o – 71o)/ sin 71o = sin 71o/ sin 71o = 1 [∵ cos (90 – θ) = sin θ]
Solution: Given, cos θ = 12/13…… (1) By definition, we know that cos θ = Base side adjacent to ∠θ / Hypotenuse……. (2) When comparing equation (1) and (2), we get Base side adjacent to ∠θ = 12 and Hypotenuse = 13 From the figure, Base side BC = 12 Hypotenuse AC = 13 Side AB is unknown here, and it caRead more
Solution:
Given, cos θ = 12/13…… (1)
By definition, we know that
cos θ = Base side adjacent to ∠θ / Hypotenuse……. (2)
When comparing equation (1) and (2), we get
Base side adjacent to ∠θ = 12 and Hypotenuse = 13
From the figure,
Base side BC = 12
Hypotenuse AC = 13
Side AB is unknown here, and it can be found by using Pythagoras theorem.
Thus, by applying Pythagoras theorem,
AC2 = AB2 + BC2
132 = AB2 + 122
Therefore,
AB2 = 132 – 122
AB2 = 169 – 144
AB2 = 25
AB = √25
AB = 5 …. (3)
Now, we know that
sin θ = Perpendicular side opposite to ∠θ / Hypotenuse
Thus, sin θ = AB/AC [from figure]
⇒ sin θ = 5/13… (4)
And, tan θ = sin θ / cos θ = (5/13) / (12/13)
⇒ tan θ = 12/13… (5)
Taking L.H.S we have
L.H.S = sin θ (1 – tan θ)
Substituting the value of sin θ and tan θ from equation (4) and (5),
Solution: Given, tan θ = a/b And we know by definition that tan θ = opposite side/ adjacent side Thus, by comparison, Opposite side = a and adjacent side = b To find the hypotenuse, we know that by Pythagoras theorem that Hypotenuse2 = opposite side2 + adjacent side2 ⇒ Hypotenuse = √(a2 + b2) So, byRead more
Solution:
Given,
tan θ = a/b
And we know by definition that
tan θ = opposite side/ adjacent side
Thus, by comparison,
Opposite side = a and adjacent side = b
To find the hypotenuse, we know that by Pythagoras theorem that
Solution: Given, 3cot A = 4 ⇒ cot A = 4/3 By definition, tan A = 1/ Cot A = 1/ (4/3) ⇒ tan A = 3/4 Thus, Base side adjacent to ∠A = 4 Perpendicular side opposite to ∠A = 3 In ΔABC, Hypotenuse is unknown. Thus, by applying Pythagoras theorem in ΔABC, We get AC2 = AB2 + BC2 AC2 = 42 + 32 AC2 = 16 + 9Read more
Solution: Given: △PQR is right-angled at Q. PQ = 4cm RQ = 3cm Required to find: sin P, sin R, sec P, sec R Given △PQR, By using Pythagoras theorem to △PQR, we get PR2 = PQ2 +RQ2 Substituting the respective values, PR2 = 42 +32 PR2 = 16 + 9 PR2 = 25 PR = √25 PR = 5 ⇒ Hypotenuse =5 By definition, sinRead more
Solution:
Given:
△PQR is right-angled at Q.
PQ = 4cm
RQ = 3cm
Required to find: sin P, sin R, sec P, sec R
Given △PQR,
By using Pythagoras theorem to △PQR, we get
PR2 = PQ2 +RQ2
Substituting the respective values,
PR2 = 42 +32
PR2 = 16 + 9
PR2 = 25
PR = √25
PR = 5
⇒ Hypotenuse =5
By definition,
sin P = Perpendicular side opposite to angle P/ Hypotenuse
sin P = RQ/ PR
⇒ sin P = 3/5
And,
sin R = Perpendicular side opposite to angle R/ Hypotenuse
Solution: Given that, sin A = 9/41 …………. (1) Required to find: cos A, tan A By definition, we know that sin A = Perpendicular/ Hypotenuse……………(2) On Comparing eq. (1) and (2), we get Perpendicular side = 9 and Hypotenuse = 41 Let’s construct △ABC as shown below, And, here the length of base AB is unRead more
Solution: By using Pythagoras theorem in △PQR, we have PR2 = PQ2 + QR2 Putting the length of given side PR and PQ in the above equation, 132 = 122 + QR2 QR2 = 132 – 122 QR2 = 169 – 144 QR2 = 25 QR = √25 = 5 By definition, tan P = Perpendicular side opposite to P/ Base side adjacent to angle P tan PRead more
Solution:
By using Pythagoras theorem in △PQR, we have
PR2 = PQ2 + QR2
Putting the length of given side PR and PQ in the above equation,
132 = 122 + QR2
QR2 = 132 – 122
QR2 = 169 – 144
QR2 = 25
QR = √25 = 5
By definition,
tan P = Perpendicular side opposite to P/ Base side adjacent to angle P
tan P = QR/PQ
tan P = 5/12 ………. (1)
And,
cot R= Base/Perpendicular
cot R= QR/PQ
cot R= 5/12 …. (2)
When comparing equation (1) and (2), we can see that R.H.S of both the equation is equal.
Therefore, L.H.S of both equations should also be equal.
1. Evaluate the following: (i) sin 20o/ cos 70o (ii) cos 19o/ sin 71o
Solution: (i) We have, sin 20o/ cos 70o = sin (90o – 70o)/ cos 70o = cos 70o/ cos70o = 1 [∵ sin (90 – θ) = cos θ] (ii) We have, cos 19o/ sin 71o = cos (90o – 71o)/ sin 71o = sin 71o/ sin 71o = 1 [∵ cos (90 – θ) = sin θ]
Solution:
(i) We have,
sin 20o/ cos 70o = sin (90o – 70o)/ cos 70o = cos 70o/ cos70o = 1 [∵ sin (90 – θ) = cos θ]
(ii) We have,
cos 19o/ sin 71o = cos (90o – 71o)/ sin 71o = sin 71o/ sin 71o = 1 [∵ cos (90 – θ) = sin θ]
See lessEvaluate each of the following: 1. sin 45∘ sin 30∘ + cos 45∘ cos 30∘
Solution:
Solution:
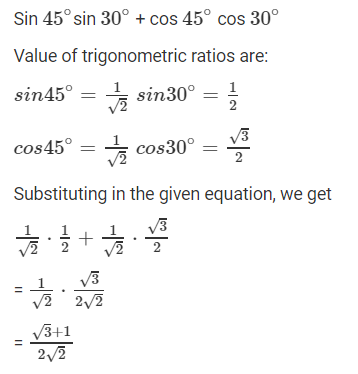
See less14. If cos θ = 12/13, show that sin θ(1 – tan θ) = 35/156
Solution: Given, cos θ = 12/13…… (1) By definition, we know that cos θ = Base side adjacent to ∠θ / Hypotenuse……. (2) When comparing equation (1) and (2), we get Base side adjacent to ∠θ = 12 and Hypotenuse = 13 From the figure, Base side BC = 12 Hypotenuse AC = 13 Side AB is unknown here, and it caRead more
Solution:
Given, cos θ = 12/13…… (1)
By definition, we know that
cos θ = Base side adjacent to ∠θ / Hypotenuse……. (2)
When comparing equation (1) and (2), we get
Base side adjacent to ∠θ = 12 and Hypotenuse = 13
From the figure,
Base side BC = 12
Hypotenuse AC = 13
Side AB is unknown here, and it can be found by using Pythagoras theorem.
Thus, by applying Pythagoras theorem,
AC2 = AB2 + BC2
132 = AB2 + 122
Therefore,
AB2 = 132 – 122
AB2 = 169 – 144
AB2 = 25
AB = √25
AB = 5 …. (3)
Now, we know that
sin θ = Perpendicular side opposite to ∠θ / Hypotenuse
Thus, sin θ = AB/AC [from figure]
⇒ sin θ = 5/13… (4)
And, tan θ = sin θ / cos θ = (5/13) / (12/13)
⇒ tan θ = 12/13… (5)
Taking L.H.S we have
L.H.S = sin θ (1 – tan θ)
Substituting the value of sin θ and tan θ from equation (4) and (5),
We get,
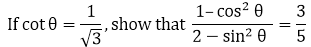
See less9. If tan θ = a/b, find the value of (cos θ + sin θ)/ (cos θ – sin θ)
Solution: Given, tan θ = a/b And we know by definition that tan θ = opposite side/ adjacent side Thus, by comparison, Opposite side = a and adjacent side = b To find the hypotenuse, we know that by Pythagoras theorem that Hypotenuse2 = opposite side2 + adjacent side2 ⇒ Hypotenuse = √(a2 + b2) So, byRead more
Solution:
Given,
tan θ = a/b
And we know by definition that
tan θ = opposite side/ adjacent side
Thus, by comparison,
Opposite side = a and adjacent side = b
To find the hypotenuse, we know that by Pythagoras theorem that
Hypotenuse2 = opposite side2 + adjacent side2
⇒ Hypotenuse = √(a2 + b2)
So, by definition
sin θ = opposite side/ Hypotenuse
sin θ = a/ √(a2 + b2)
And,
cos θ = adjacent side/ Hypotenuse
cos θ = b/ √(a2 + b2)
Now,
After substituting for cos θ and sin θ, we have
∴
Hence, proved.
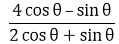
See less9. If tan θ = a/b, find the value of (cos θ + sin θ)/ (cos θ – sin θ)
Solution: Given, 3cot A = 4 ⇒ cot A = 4/3 By definition, tan A = 1/ Cot A = 1/ (4/3) ⇒ tan A = 3/4 Thus, Base side adjacent to ∠A = 4 Perpendicular side opposite to ∠A = 3 In ΔABC, Hypotenuse is unknown. Thus, by applying Pythagoras theorem in ΔABC, We get AC2 = AB2 + BC2 AC2 = 42 + 32 AC2 = 16 + 9Read more
Solution:
Given,
3cot A = 4
⇒ cot A = 4/3
By definition,
tan A = 1/ Cot A = 1/ (4/3)
⇒ tan A = 3/4
Thus,
Base side adjacent to ∠A = 4
Perpendicular side opposite to ∠A = 3
In ΔABC, Hypotenuse is unknown.
Thus, by applying Pythagoras theorem in ΔABC,
We get
AC2 = AB2 + BC2
AC2 = 42 + 32
AC2 = 16 + 9
AC2 = 25
AC = √25
AC = 5
Hence, hypotenuse = 5
Now, we can find that
sin A = opposite side to ∠A/ Hypotenuse = 3/5
And,
cos A = adjacent side to ∠A/ Hypotenuse = 4/5
Taking the LHS,
Thus, LHS = 7/25
Now, taking RHS,
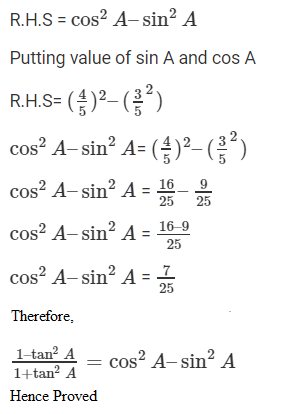
See less7. If cot θ = 7/8, evaluate (i) (1+sin θ)(1–sin θ)/ (1+cos θ)(1–cos θ) (ii) cot2 θ
Solution: (i) Required to evaluate: , given = cot θ = 7/8 Taking the numerator, we have (1+sin θ)(1–sin θ) = 1 – sin2 θ [Since, (a+b)(a-b) = a2 – b2] Similarly, (1+cos θ)(1–cos θ) = 1 – cos2 θ We know that, sin2 θ + cos2 θ = 1 ⇒ 1 – cos2 θ = sin2 θ And, 1 – sin2 θ = cos2 θ Thus, (1+sin θ)(1 –sin θ)Read more
Solution:
(i) Required to evaluate:
, given = cot θ = 7/8
Taking the numerator, we have
(1+sin θ)(1–sin θ) = 1 – sin2 θ [Since, (a+b)(a-b) = a2 – b2]
Similarly,
(1+cos θ)(1–cos θ) = 1 – cos2 θ
We know that,
sin2 θ + cos2 θ = 1
⇒ 1 – cos2 θ = sin2 θ
And,
1 – sin2 θ = cos2 θ
Thus,
(1+sin θ)(1 –sin θ) = 1 – sin2 θ = cos2 θ
(1+cos θ)(1–cos θ) = 1 – cos2 θ = sin2 θ
⇒
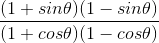
= cos2 θ/ sin2 θ
= (cos θ/sin θ)2
And, we know that (cos θ/sin θ) = cot θ
⇒
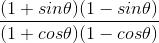
= (cot θ)2
= (7/8)2
= 49/ 64
(ii) Given,
cot θ = 7/8
So, by squaring on both sides we get
(cot θ)2 = (7/8)2
∴ cot θ2 = 49/64
See less6. In △PQR, right-angled at Q, PQ = 4cm and RQ = 3 cm. Find the value of sin P, sin R, sec P and sec R.
Solution: Given: △PQR is right-angled at Q. PQ = 4cm RQ = 3cm Required to find: sin P, sin R, sec P, sec R Given △PQR, By using Pythagoras theorem to △PQR, we get PR2 = PQ2 +RQ2 Substituting the respective values, PR2 = 42 +32 PR2 = 16 + 9 PR2 = 25 PR = √25 PR = 5 ⇒ Hypotenuse =5 By definition, sinRead more
Solution:
Given:
△PQR is right-angled at Q.
PQ = 4cm
RQ = 3cm
Required to find: sin P, sin R, sec P, sec R
Given △PQR,
By using Pythagoras theorem to △PQR, we get
PR2 = PQ2 +RQ2
Substituting the respective values,
PR2 = 42 +32
PR2 = 16 + 9
PR2 = 25
PR = √25
PR = 5
⇒ Hypotenuse =5
By definition,
sin P = Perpendicular side opposite to angle P/ Hypotenuse
sin P = RQ/ PR
⇒ sin P = 3/5
And,
sin R = Perpendicular side opposite to angle R/ Hypotenuse
sin R = PQ/ PR
⇒ sin R = 4/5
And,
sec P=1/cos P
secP = Hypotenuse/ Base side adjacent to ∠P
sec P = PR/ PQ
⇒ sec P = 5/4
Now,
sec R = 1/cos R
secR = Hypotenuse/ Base side adjacent to ∠R
sec R = PR/ RQ
⇒ sec R = 5/3
See less4. If sin A = 9/41, compute cos A and tan A.
Solution: Given that, sin A = 9/41 …………. (1) Required to find: cos A, tan A By definition, we know that sin A = Perpendicular/ Hypotenuse……………(2) On Comparing eq. (1) and (2), we get Perpendicular side = 9 and Hypotenuse = 41 Let’s construct △ABC as shown below, And, here the length of base AB is unRead more
Solution:
Given that, sin A = 9/41 …………. (1)
Required to find: cos A, tan A
By definition, we know that
sin A = Perpendicular/ Hypotenuse……………(2)
On Comparing eq. (1) and (2), we get
Perpendicular side = 9 and Hypotenuse = 41
Let’s construct △ABC as shown below,
And, here the length of base AB is unknown.
Thus, by using Pythagoras theorem in △ABC, we get
AC2 = AB2 + BC2
412 = AB2 + 92
AB2 = 412 – 92
AB2 = 168 – 81
AB= 1600
AB = √1600
AB = 40
⇒ Base of triangle ABC, AB = 40
We know that,
cos A = Base/ Hypotenuse
cos A =AB/AC
cos A =40/41
And,
tan A = Perpendicular/ Base
tan A = BC/AB
tan A = 9/40
See less3. In fig. 5.37, find tan P and cot R. Is tan P = cot R?
Solution: By using Pythagoras theorem in △PQR, we have PR2 = PQ2 + QR2 Putting the length of given side PR and PQ in the above equation, 132 = 122 + QR2 QR2 = 132 – 122 QR2 = 169 – 144 QR2 = 25 QR = √25 = 5 By definition, tan P = Perpendicular side opposite to P/ Base side adjacent to angle P tan PRead more
Solution:
By using Pythagoras theorem in △PQR, we have
PR2 = PQ2 + QR2
Putting the length of given side PR and PQ in the above equation,
132 = 122 + QR2
QR2 = 132 – 122
QR2 = 169 – 144
QR2 = 25
QR = √25 = 5
By definition,
tan P = Perpendicular side opposite to P/ Base side adjacent to angle P
tan P = QR/PQ
tan P = 5/12 ………. (1)
And,
cot R= Base/Perpendicular
cot R= QR/PQ
cot R= 5/12 …. (2)
When comparing equation (1) and (2), we can see that R.H.S of both the equation is equal.
Therefore, L.H.S of both equations should also be equal.
∴ tan P = cot R
Yes, tan P = cot R = 5/12
See less