This is the basic and conceptual question from Chapter name- circles
Topic – Angle properties of circles
Chapter number- 15
In this question we have been given the figure of circle with certain information about the figure and we have to find <PQB im first figure, and <CEF, <COF in second figure
ICSE Avichal publication
Understanding ICSE Mathematics
Question 6



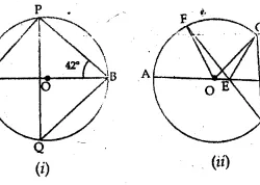

Solution:
In ∆APB,
∠APB = 90° (Angle in a semi-circle)
But ∠A + ∠APB + ∠ABP = 180° (Angles of a triangle)
∠A + 90° + 42°= 180°
∠A + 132° = 180°
⇒ ∠A = 180° – 132° = 48°
But
∠A = ∠PQB
(Angles in the same segment of a circle)
∠PQB = 48o
(b) (i) in ∆EDC,
(Ext, angle of a triangle is equal to the sum
of its interior opposite angels)
(ii) arc CF subtends ∠COF at the centre and
∠CDF at the remaining part of the circle
∠COF = 2 ∠CDF = 2 ∠CDE
=2 × 32o = 2 ∠CDE
= 2 × 32o = 64o