a bit typical question, provide an easy solution to it, how should i approach???
n the figure, BDC is a tangent to the given circle at point D such that BD = 30 to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF (ii) radius of the circle.
Share



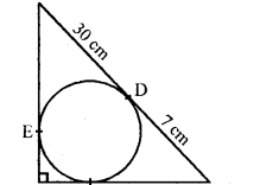

In the figure, BDC is a tangent to the given circle with centre O and D is a point such that


BD = 30 cm and CD = 7 cm
BE and CF are other two tangents drawn from B and C respectively which meet at A on producing this and ∆BAC is a right angle so formed
To find : (i) AF and (ii) radius of the circle
Join OE and OF
OE = OF radii of the circle
OE ⊥ AB and OF ⊥ AC
OEAF is a square
BD and BE are the tangents from B
BE = BD = 30 cm and similarly
CF = CD = 7 cm
Let r be the radius of the circle
OF = AF = AE = r
AB = 30 + r and AC = 7 + r and BC = 30 + 7 = 37 cm
Now in right ∆ABC