sir this is the important question from the book -ML aggarwal( avichal publication) class 10th , chapter20 , heights and distances
it is given that In the adjoining figure, the shadow of a vertical tower on the level ground increases by 10 m, when the altitude of the sun changes from 45 to 30.
Find the height of the tower and give your answer, correct to 1/10 of a metre.
question no 37 , heights and distances , ICSE board, ML Aggarwal



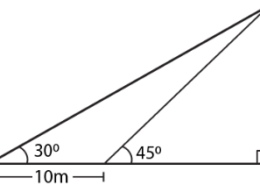

Consider TR as the tower where TR = h
BR = x
AB = 10 m
Angles of elevation from the top of the tower at A and B are 300 and 450
In right triangle TAR
tan θ = TR/AR
Substituting the values
tan 300 = h/ (10 + x)
So we get
1/√3 = h/ (10 + x)
h = (10 + x)/ √3 …. (1)
In triangle TBR
tan 450 = TR/BR = h/x
So we get
1 = h/x
x = h ….. (2)
Using both the equations
h = (10 + h)/ √3
√3h = 10 + h
By further calculation
√3h – h = 10
(1.732 – 1) h = 10
0.732 h = 10
h = 10/0.732 = 13.66
Hence, the height of the tower is 13.7 m.