Hello sir i want to know the best solution of the question from exercise 8.1of math of Quadrilaterals chapter of class 9th give me the best and easy for solving this question how i solve it of question no. 9 In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that: (iii) ΔAQB ≅ ΔCPD (iv) AQ = CP
AnilSinghBoraGuru
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that: (iii) ΔAQB ≅ ΔCPD (iv) AQ = CP Q.9(3-4)
Share



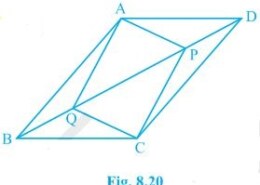

(iii) In ΔAQB and ΔCPD,
BQ = DP (Given)
∠ABQ = ∠CDP (Alternate interior angles)
AB = CD (Opposite sides of a parallelogram)
Thus, ΔAQB ≅ ΔCPD [SAS congruency]
(iv) As ΔAQB ≅ ΔCPD
AQ = CP [CPCT]