In the class 10th maths book in triangles chapter of exercise 6.6 of ncert how i solve this problem in easy and simple way because it very important for class 10th also In Figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that : (iii) AC2 + AB2 = 2 AD2 + ½ BC2
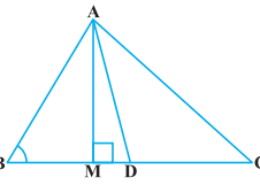
By applying Pythagoras Theorem in ∆ABM, we get,
AM2 + MB2 = AB2 ………………….… (i)
By applying Pythagoras Theorem in ∆AMC, we get,
AM2 + MC2 = AC2 …………………..… (ii)
Adding both the equations (i) and (ii), we get,
2AM2 + MB2 + MC2 = AB2 + AC2
2AM2 + (BD − DM) 2 + (MD + DC) 2 = AB2 + AC2
2AM2+BD2 + DM2 − 2BD.DM + MD2 + DC2 + 2MD.DC = AB2 + AC2
2AM2 + 2MD2 + BD2 + DC2 + 2MD (− BD + DC) = AB2 + AC2
2(AM2+ MD2) + (BC/2) 2 + (BC/2) 2 + 2MD (-BC/2 + BC/2) 2 = AB2 + AC2
2AD2 + BC2/2 = AB2 + AC2