How can i solve this tough question of class 9th ncert of Areas of Parallelograms and Triangles of math of exercise 9.4 of question no.8(5). Give me the best and simple way for solving this question. In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ^ DE meets BC at Y. Show that:(v) ar(CYXE) = 2ar(FCB)
AnilSinghBoraGuru
In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ^ DE meets BC at Y. Show that:(v) ar(CYXE) = 2ar(FCB) Q.8(5)
Share



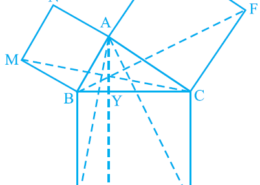

AX ⊥ DE and CE ⊥ DE (Adjacent sides of square BDEC) [given]
Hence,
CE || AX (Two lines perpendicular to the same line are parallel to each other)
Consider BACE and parallelogram CYXE
BACE and parallelogram CYXE are on the same base CE and between the same parallels CE and AX.
∴ar (∆YXE) = 2ar (∆ACE) … (iv)
We had proved that
∴ ∆FCB ≅ ∆ACE
ar (∆FCB) ≅ ar (∆ACE) … (v)
From equations (iv) and (v), we get
ar (CYXE) = 2 ar (∆FCB) … (vi)