What is the easiest way for solving the question of class 9th ncert math of exercise 9.4of math of Areas of Parallelograms and Triangles chapter of question no.8(2) Please help me for the best suggestion of this question In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ^ DE meets BC at Y. Show that: Ncert solutions class 9 chapter 9-38 (ii) ar(BYXD) = 2ar(MBC)
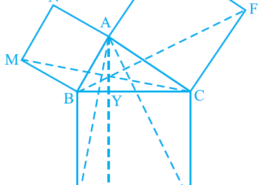
We have
∆MBC ≅ ∆ABD
∴ar (∆MBC) = ar (∆ABD) … (i)
It is given that AX ⊥ DE and BD ⊥ DE (Adjacent sides of square BDEC)
∴ BD || AX (Two lines perpendicular to same line are parallel to each other)
∆ABD and parallelogram BYXD are on the same base BD and between the same parallels BD and AX.
Area (∆YXD) = 2 Area (∆MBC) [From equation (i)] … (ii)