What is the easiest way for solving the question of class 9th ncert math of exercise 9.4 of math of Areas of Parallelograms and Triangles chapter of question no.5(6)Please help me for the best suggestion of this question In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:(vi) ar (FED) = 1/8 ar (AFC)
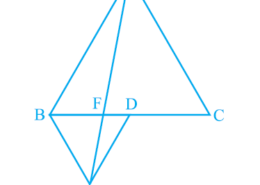
ar (ΔAFC) = ar (ΔAFD) + ar(ΔADC)
= 2 ar (ΔFED) + (1/2) ar(ΔABC) [using (v)
= 2 ar (ΔFED) + ½ [4ar(ΔBDE)] [Using result of Question (i)]
= 2 ar (ΔFED) +2 ar(ΔBDE)
Since, ΔBDE and ΔAED are on the same base and between same parallels
= 2 ar (ΔFED) +2 ar (ΔAED)
= 2 ar (ΔFED) +2 [ar (ΔAFD) +ar (ΔFED)]
= 2 ar (ΔFED) +2 ar (ΔAFD) +2 ar (ΔFED) [From question (viii)]
= 4 ar (ΔFED) +4 ar (ΔFED)
⇒ar (ΔAFC) = 8 ar (ΔFED)
⇒ar (ΔFED) = (1/8) ar (ΔAFC)
Hence proved