what is the tricky way for solving the question of class 9th ncert math of Areas of Parallelograms and Triangles chapter of ncert of exercise 9.4 of math give me the best and simple way for solving this question in easy and simple way In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:(v) ar (BFE) = 2 ar (FED)
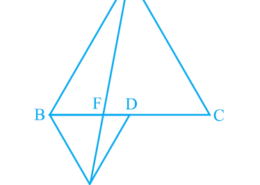
Assume that h is the height of vertex E, corresponding to the side BD in ΔBDE.
Also assume that H is the height of vertex A, corresponding to the side BC in ΔABC.
While solving Question (i),
We saw that,
ar (ΔBDE) = ¼ ar (ΔABC)
While solving Question (iv),
We saw that,
ar (ΔBFE) = ar (ΔAFD).
∴ar (ΔBFE) = ar (ΔAFD)
= 2 ar (ΔFED)
Hence, ar (ΔBFE) = 2 ar (ΔFED)
Hence proved