How i solve the question of class 9th ncert math of Areas of Parallelograms and Triangles chapter of exercise 9.3of question no 16. I think it is very important question of class 9th give me the tricky way for solving this question In Fig.9.29, ar(DRC) = ar(DPC) and ar(BDP) = ar(ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
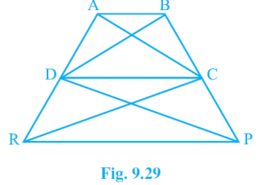
Given,
ar(△DRC) = ar(△DPC)
ar(△BDP) = ar(△ARC)
To Prove,
ABCD and DCPR are trapeziums.
Proof:
ar(△BDP) = ar(△ARC)
⇒ ar(△BDP) – ar(△DPC) = ar(△DRC)
⇒ ar(△BDC) = ar(△ADC)
ar(△BDC) = ar(△ADC).
∴, ar(△BDC) and ar(△ADC) are lying in-between the same parallel lines.
∴, AB ∥ CD
ABCD is a trapezium.
Similarly,
ar(△DRC) = ar(△DPC).
∴, ar(△DRC) andar(△DPC) are lying in-between the same parallel lines.
∴, DC ∥ PR
∴, DCPR is a trapezium.