I want to know the best answer of the question from Areas of Parallelograms and Triangles chapter of class 9th ncert math. The question from exercise 9.3of math. Give me the easy way for solving this question of 6(1) In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that: (i) ar (DOC) = ar (AOB)
AnilSinghBoraGuru
In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that: (i) ar (DOC) = ar (AOB) Q.6(1)
Share



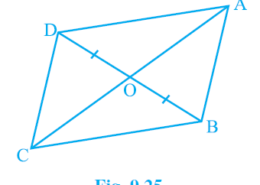

Given,
OB = OD and AB = CD
Construction,
DE ⊥ AC and BF ⊥ AC are drawn.
Proof:
(i) In ΔDOE and ΔBOF,
∠DEO = ∠BFO (Perpendiculars)
∠DOE = ∠BOF (Vertically opposite angles)
OD = OB (Given)
∴, ΔDOE ≅ ΔBOF by AAS congruence condition.
∴, DE = BF (By CPCT) — (i)
also, ar(ΔDOE) = ar(ΔBOF) (Congruent triangles) — (ii)
Now,
In ΔDEC and ΔBFA,
∠DEC = ∠BFA (Perpendiculars)
CD = AB (Given)
DE = BF (From i)
∴, ΔDEC ≅ ΔBFA by RHS congruence condition.
∴, ar(ΔDEC) = ar(ΔBFA) (Congruent triangles) — (iii)
Adding (ii) and (iii),
ar(ΔDOE) + ar(ΔDEC) = ar(ΔBOF) + ar(ΔBFA)
⇒ ar (DOC) = ar (AOB)