Yesterday i was doing the question from class 9th ncert book of math of Areas of Parallelograms and Triangles chapter of exercise 9.3 What is the easiest way for solving it because i was not able to do this question please help me for solving this question In Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar(ACE)
AnilSinghBoraGuru
In Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar(ACE). Q.1
Share



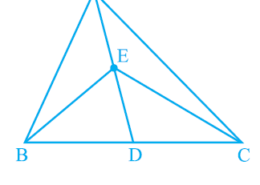

Given,
AD is median of ΔABC. ∴, it will divide ΔABC into two triangles of equal area.
∴ar(ABD) = ar(ACD) — (i)
also,
ED is the median of ΔABC.
∴ar(EBD) = ar(ECD) — (ii)
Subtracting (ii) from (i),
ar(ABD) – ar(EBD) = ar(ACD) – ar(ECD)
⇒ar(ABE) = ar(ACE)