I want to know the best answer of the question from Lines and Angles chapter of class 9th ncert math. The question from exercise 6.3of math. Give me the easy way for solving this question of 2
AnilSinghBoraGuru
In Fig. 6.40, X = 62°, XYZ = 54°. If YO and ZO are the bisectors of XYZ and XZY respectively of Δ XYZ, find OZY and YOZ. Q.2
Share



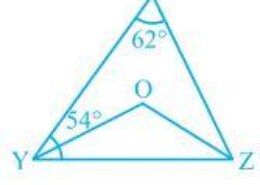

We know that the sum of the interior angles of the triangle.
So, X +XYZ +XZY = 180°
Putting the values as given in the question we get,
62°+54° +XZY = 180°
Or, XZY = 64°
Now, we know that ZO is the bisector so,
OZY = ½ XZY
∴ OZY = 32°
Similarly, YO is a bisector and so,
OYZ = ½ XYZ
Or, OYZ = 27° (As XYZ = 54°)
Now, as the sum of the interior angles of the triangle,
OZY +OYZ +O = 180°
Putting their respective values, we get,
O = 180°-32°-27°
Hence, O = 121°