Home/ Questions/Q 11549
In Process
Adv
AnilSinghBora
  • 0
Guru
Asked: 2021-08-10T13:10:39+05:30 In:

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that (i) ΔAPB ≅ ΔCQD (ii) AP = CQ Q.10

  • 0
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that (i) ΔAPB ≅ ΔCQD (ii) AP = CQ Q.10

What is the easiest way for solving the question of class 9th ncert math of exercise 8.1of math of Quadrilaterals chapter of question no 10  Please help me for the best suggestion of this question  ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that (i) ΔAPB ≅ ΔCQD (ii) AP = CQ

best math ncert solutionexercise 8.1 ncertncert class 9th solutionquadrilaterals ncert
Share

    1 Answer

    1. Guru

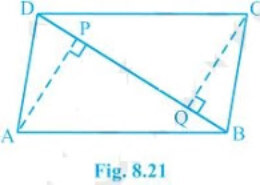
      (i) In ΔAPB and ΔCQD,

      ∠ABP = ∠CDQ (Alternate interior angles)

      ∠APB = ∠CQD (= 90o as AP and CQ are perpendiculars)

      AB = CD (ABCD is a parallelogram)

      , ΔAPB ≅ ΔCQD [AAS congruency]

      (ii) As ΔAPB ≅ ΔCQD.

      , AP = CQ [CPCT]

      • 0
    Leave an answer

    Leave an answer

    Browse

    Choose from here the video type.

    Put Video ID here: https://www.youtube.com/watch?v=sdUUx5FdySs Ex: "sdUUx5FdySs".

    Captcha Click on image to update the captcha.

    Related Questions

    Adv