Please suggest me the best way to solve the problem of question from circles chapter of exercise 10.2 of ncert math of question no.12 how i solve this problem in easy and simple way A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC.
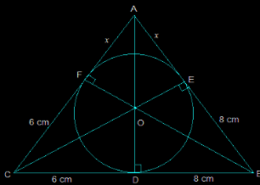
The figure given is as follows:
Consider the triangle ABC,
We know that the length of any two tangents which are drawn from the same point to the circle is equal.
So,
(i) CF = CD = 6 cm
(ii) BE = BD = 8 cm
(iii) AE = AF = x
Now, it can be observed that,
(i) AB = EB+AE = 8+x
(ii) CA = CF+FA = 6+x
(iii) BC = DC+BD = 6+8 = 14
Now the semi perimeter “s” will be calculated as follows
2s = AB+CA+BC
By putting the respective values we get,
2s = 28+2x
s = 14+x
By solving this we get,
= √(14+x)48x ……… (i)
Again, the area of △ABC = 2 × area of (△AOF + △COD + △DOB)
= 2×[(½×OF×AF)+(½×CD×OD)+(½×DB×OD)]
= 2×½(4x+24+32) = 56+4x …………..(ii)
Now from (i) and (ii) we get,
√(14+x)48x = 56+4x
Now, square both the sides,
48x(14+x) = (56+4x)2
48x = [4(14+x)]2/(14+x)
48x = 16(14+x)
48x = 224+16x
32x = 224
x = 7 cm
So, AB = 8+x
i.e. AB = 15 cm
And, CA = x+6 =13 cm.