How i complete this question of class 10th ncert of Probability chapter of exercise 15.1 of both question of 22, this is tough question of this chapter give me the best way for solving this problem A student argues that ‘there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability 1/11. Do you agree with this argument? Justify your Solution:.
If 2 dices are thrown, the possible events are:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
So, the total numbers of events: 6×6 = 36
(i) It is given that to get the sum as 2, the probability is 1/36 as the only possible outcomes = (1,1)
For getting the sum as 3, the possible events (or outcomes) = E (sum 3) = (1,2) and (2,1)
So, P(sum 3) = 2/36
Similarly,
E (sum 4) = (1,3), (3,1), and (2,2)
So, P (sum 4) = 3/36
E (sum 5) = (1,4), (4,1), (2,3), and (3,2)
So, P (sum 5) = 4/36
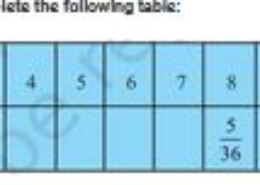
E (sum 6) = (1,5), (5,1), (2,4), (4,2), and (3,3)
So, P (sum 6) = 5/36
E (sum 7) = (1,6), (6,1), (5,2), (2,5), (4,3), and (3,4)
So, P (sum 7) = 6/36
E (sum 8) = (2,6), (6,2), (3,5), (5,3), and (4,4)
So, P (sum 8) = 5/36
E (sum 9) = (3,6), (6,3), (4,5), and (5,4)
So, P (sum 9) = 4/36
E (sum 10) = (4,6), (6,4), and (5,5)
So, P (sum 10) = 3/36
E (sum 11) = (5,6), and (6,5)
So, P (sum 11) = 2/36
E (sum 12) = (6,6)
So, P (sum 12) = 1/36
So, the table will be as: