The question from class 10th ncert book of exercise 10.2 of question no.8 of circles chapter, how i solve this question in easy way i think it is very important for class 10th, A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC
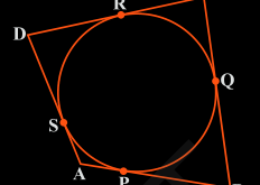
The figure given is:
From this figure we can conclude a few points which are:
(i) DR = DS
(ii) BP = BQ
(iii) AP = AS
(iv) CR = CQ
Since they are tangents on the circle from points D, B, A, and C respectively.
Now, adding the LHS and RHS of the above equations we get,
DR+BP+AP+CR = DS+BQ+AS+CQ
By rearranging them we get,
(DR+CR) + (BP+AP) = (CQ+BQ) + (DS+AS)
By simplifying,
AD+BC= CD+AB