Find the simplest method to solve the ncert class 10 chapter surface areas and volumes give me the best solution of the question exercise 13.1 question number 4. Give me the simplest and easiest form to solve the question also find the formula which is put in this question. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig.).
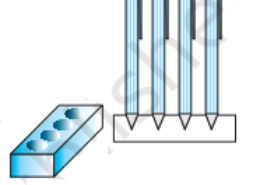
Volume of cuboid = length x width x height
We know the cuboid’s dimensions as 15 cmx10 cmx3.5 cm
So, the volume of the cuboid = 15x10x3.5 = 525 cm3
Here, depressions are like cones and we know,
Volume of cone = (⅓)πr2h
Given, radius (r) = 0.5 cm and depth (h) = 1.4 cm
∴ Volume of 4 cones = 4x(⅓)πr2h
= 1.46 cm2
Now, volume of wood = Volume of cuboid – 4 x volume of cone
= 525-1.46 = 523.54 cm2