0 mehakNewbie Asked: June 24, 20232023-06-24T20:39:22+05:30 2023-06-24T20:39:22+05:30In: CBSE 7. If cot θ = 7/8, evaluate (i) (1+sin θ)(1–sin θ)/ (1+cos θ)(1–cos θ) (ii) cot2 θ 0 Explain the question. Justify the answer Class 10th, rd sharma, trigonometric identities rd sharma class 10thtrigonometric identities Share Facebook 1 Answer Voted Oldest Recent mehak Newbie 2023-06-25T19:50:42+05:30Added an answer on June 25, 2023 at 7:50 pm Solution: (i) Required to evaluate: , given = cot θ = 7/8 Taking the numerator, we have (1+sin θ)(1–sin θ) = 1 – sin2 θ [Since, (a+b)(a-b) = a2 – b2] Similarly, (1+cos θ)(1–cos θ) = 1 – cos2 θ We know that, sin2 θ + cos2 θ = 1 ⇒ 1 – cos2 θ = sin2 θ And, 1 – sin2 θ = cos2 θ Thus, (1+sin θ)(1 –sin θ) = 1 – sin2 θ = cos2 θ (1+cos θ)(1–cos θ) = 1 – cos2 θ = sin2 θ ⇒ = cos2 θ/ sin2 θ = (cos θ/sin θ)2 And, we know that (cos θ/sin θ) = cot θ ⇒ = (cot θ)2 = (7/8)2 = 49/ 64 (ii) Given, cot θ = 7/8 So, by squaring on both sides we get (cot θ)2 = (7/8)2 ∴ cot θ2 = 49/64 0 Reply Share Share Share on Facebook Share on Twitter Share on LinkedIn Share on WhatsApp Leave an answerLeave an answerCancel reply Featured image Select file Browse Add a Video to describe the problem better. Video type Youtube Vimeo Dailymotion Facebook Choose from here the video type. Video ID Put Video ID here: https://www.youtube.com/watch?v=sdUUx5FdySs Ex: "sdUUx5FdySs". Click on image to update the captcha. Visual Code Save my name, email, and website in this browser for the next time I comment. Related Questions 16. A copper sphere of radius 3 cm is melted and recast into a right circular cone of ... 17. A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of ... 18. The diameters of the internal and external surfaces of a hollow spherical shell are 10cm and 6 ... 19. How many coins 1.75 cm in diameter and 2 mm thick must be melted to form a ... 20. The surface area of a solid metallic sphere is 616 cm2. It is melted and recast into ...
Solution:
(i) Required to evaluate:
 , given = cot θ = 7/8
, given = cot θ = 7/8
Taking the numerator, we have
(1+sin θ)(1–sin θ) = 1 – sin2 θ [Since, (a+b)(a-b) = a2 – b2]
Similarly,
(1+cos θ)(1–cos θ) = 1 – cos2 θ
We know that,
sin2 θ + cos2 θ = 1
⇒ 1 – cos2 θ = sin2 θ
And,
1 – sin2 θ = cos2 θ
Thus,
(1+sin θ)(1 –sin θ) = 1 – sin2 θ = cos2 θ
(1+cos θ)(1–cos θ) = 1 – cos2 θ = sin2 θ
⇒
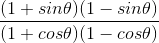
= cos2 θ/ sin2 θ
= (cos θ/sin θ)2
And, we know that (cos θ/sin θ) = cot θ
⇒
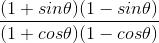
= (cot θ)2
= (7/8)2
= 49/ 64
(ii) Given,
cot θ = 7/8
So, by squaring on both sides we get
(cot θ)2 = (7/8)2
∴ cot θ2 = 49/64