Please give me the best way to solve the problem of Class 10th math of ncert of triangles chapter of exercise 6.6, Give me the easiest way to solve this problem In Figure, two chords AB and CD intersect each other at the point P. Prove that : (i) ∆APC ~ ∆ DPB (ii) AP . PB = CP . DP
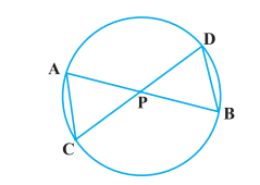
Firstly, let us join CB, in the given figure.
(i) In ∆APC and ∆DPB,
∠APC = ∠DPB (Vertically opposite angles)
∠CAP = ∠BDP (Angles in the same segment for chord CB)
Therefore,
∆APC ∼ ∆DPB (AA similarity criterion)
(ii) In the above, we have proved that ∆APC ∼ ∆DPB
We know that the corresponding sides of similar triangles are proportional.
∴ AP/DP = PC/PB = CA/BD
⇒AP/DP = PC/PB
∴AP. PB = PC. DP
Hence, proved.