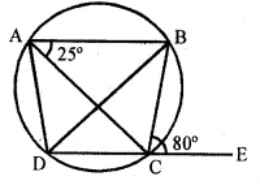
(b) in the figure, AB ∥DC

∠BCE = 80^o and ∠BAC = 25^o

ABCD is a cyclic Quadrilateral and DC is

Production to E

(i) Ext, ∠BCE = interior ∠A

80^o = ∠BAC + ∠CAD

80^o = 25^o + ∠CAD

∠CAD = 80^o – 25^o = 55^o

(ii) But ∠CAD = ∠CBD

(Alternate angels)

∠CBD = 55^o

(iii) ∠BAC = ∠BDC

(Angles in the same segments)

∠BDC = 25^o

(∠BAC = 25^o)

Now AB ∥ DC and BD is the transversal

∠BDC = ∠ABD

∠ABD = 25^o

∠ABC = ∠ABD + ∠CBD = 25^o + 55^o = 80^o

But ∠ABC + ∠ADC = 180^o

(opposite angles of a cyclic quadrilateral)

80^o + ∠ADC = 180^o

∠ADC = 180^o – 80^o = 100^o