In the figure, it is given that AB=AC and p is a point somewhere on BC such that PM⊥AB and PN⊥AC and we have been asked to prove that BM×NP=CN×MP using the properties of similarities
ML Aggarwal, Avichal publication, class 10, Similarity, chapter 13, question no 11



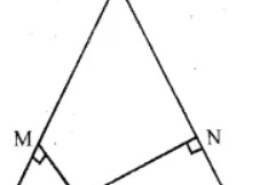

From the question it is given that, ABC is a triangle in which AB=AC.
P is a point on the side BC such that PM⊥AB and PN⊥AC.
We have to prove that, BM×NP=CN×MP
Consider the △ABC
AB=AC … [from the question]
∠B=∠C … [angles opposite to equal sides]
Then, consider △BMP and △CNP
∠M=∠N
Therefore, △BMP∼△CNP
So, BM/CN=MP/NP
By cross multiplication we get,
BM×NP=CN×MP
Hence it is proved.