In the given figure, AB and DE are perpendicular to BC. (i) Prove that ΔABC ~ ΔDEC (ii) If AB = 6 cm DE = 4 cm and AC = 15 cm. Calculate CD. (iii) Find the ratio of the area of ΔABC : are a of ΔDEC

Question

Rajan@2021Guru

Asked: March 27, 20212021-03-27T15:47:24+05:30 2021-03-27T15:47:24+05:30In: ICSE

In the given figure, AB and DE are perpendicular to BC.

(i) Prove that ΔABC ~ ΔDEC

(ii) If AB = 6 cm DE = 4 cm and AC = 15 cm. Calculate CD.

(iii) Find the ratio of the area of ΔABC : are a of ΔDEC

ML Aggarwal Avichal Publication class 10, similarity chapter 13.3, question no 8

Leave an answer

MathsMentor · Answer 1 · 2021-03-27T16:20:16+05:30

MathsMentor Guru

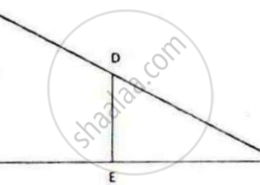
(i) From ΔABC and ΔDEC,
∠ABC=∠DEC=90∘ (Given)
and ∠ACB=∠DCE= Common
∴ ΔABC∼ΔDEC (By A−A similarity)
(ii) In ΔABC and ΔDEC,
ΔABC∼ΔDEC (proved in (i) part)
∴AB/DE=AC/CD
Given: AB=6 cm,DE=4 cm,AC=15 cm,
∴6/4=15/CD
⇒6×CD=15×4
⇒CD=60/6
⇒CD=10 cm.
(iii) Area of ΔDECArea of ΔABC=AB2/DE2 (∵ΔABC∼ΔDEC)
=(4)2(6)2=36/16=9/4
∴ Area of ΔABC: Area of ΔDEC=9:4