In the figure given below, ∠ABC=∠DAC and AB=8cm,AC=4cm,AD=5cm. (i) Prove that △ACD is similar to △BCA (ii) Find BC and CD (iii) Find the area of △ACD : area of △ABC.

Question

Rajan@2021Guru

Asked: March 28, 20212021-03-28T21:07:32+05:30 2021-03-28T21:07:32+05:30In: ICSE

This is the basic and conceptual question from similarity chapter in which we are to

(i) Prove that △ACD is similar to △BCA

(ii) Find BC and CD

(iii) Find the area of △ACD : area of △ABC.

We have given a figure of triangle in which ∠ABC=∠DAC and AB=8cm,AC=4cm,AD=5cm

Leave an answer

MathsMentor · Answer 1 · 2021-03-28T23:30:50+05:30

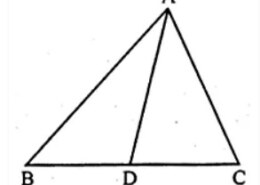
From the question it is given that,
∠ABC=∠DAC
AB=8cm,AC=4cm,AD=5cm
(i) Now, consider △ACD and △BCA
∠C=∠C … [common angle for both triangles]
∠ABC=∠CAD … [from the question]
So, △ACD∼△BCA … [by AA axiom]
(ii) AC/BC=CD/CA=AD/AB
Consider AC/BC=AD/AB
4/BC=5/8
BC=(4×8)/5
BC=32/5
BC=6.4cm
Then, consider CD/CA=AD/AB
CD/4=5/8
CD=(4×5)/8
CD=20/8
CD=2.5cm
(iii) from (i) we proved that, △ACD∼△BCA
area of △ACB/area of △BCA=AC2/AB2
=42/82
=16/64
By dividing both numerator and denominator by 16, we get,
=41
Therefore, the area of △ACD : area of △ABC is 1:4.