An important question from ML Aggarwal of similarity chapter in which we have been asked to find the ratio of DE:BC by using the basic proportionality theorem if DE∥BC and the ratio of the areas of △ADE and trapezium DBCE is 4:5.
ML Aggarwal Avichal Publication chapter 13.3, question no 13.a



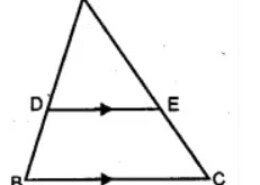

From the question it is given that,
DE∥BC
The ratio of the areas of △ADE and trapezium DBCE is 4:5
Now, consider the △ABC and △ADE
∠A=∠A … [common angle for both triangles]
∠D=∠B and ∠E=∠C … [because corresponding angles are equal]
Therefore, △ADE∼△ABC
So, area of △ADE/area of △ABC=(DE)2/(BC)2 … [equation (i)]
Then, area of △ADE/area of trapezium DBCE=4/5
area of trapezium DBCE/area of △ADE=5/4
Add 1 for both LHS and RHS we get,
(area of trapezium DBCE/area of △ADE)+1=(5/4)+1
(area of trapezium DBCE+ area of △ADE)/area of △ADE=(5+4)/4
area of △ABC/area of △ADE=9/4
area of △ADE/area of △ABC=4/9
From equation (i),
area of △ADE/area of △ABC=(DE)2/(BC)2
area of △ADE/area of △ABC=(DE)2/(BC)2=42/92
area of △ADE/area of △ABC=(DE)2/(BC)2=2/3
Therefore, DE:BC=2:3