In the given figure we have been given the length of sides AO=10 cm,OC=5 cm,AB=6.5 cm and OD=2.8 cm and we are to
(i) Prove that △OAB∼△OCD.
(ii) Find CD and OB
(iii) Calculate the ratio of areas of △OAB and △OCD
ML Aggarwal, Avichal Publication, class 10, Similarity, chapter 13.3, question no 5b



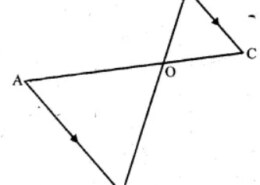

From the question it is given that,
AB∥DC.AO=10cm,OC=5cm,AB=6.5cm and OD=2.8cm
(i) We have to prove that, △OAB∼△OCD
So, consider the △OAB and △OCD
∠AOB=∠COD … [because vertically opposite angles are equal]
∠OBA=∠OCD … [because alternate angles are equal]
Therefore, △OAB∼△OCD … [from AAA axiom]
(ii) Consider the △OAB and △OCD
OA/OC=OB/OD=AB/CD
Now consider OA/OC=OB/OD
10/5=OB/2.8
OB=(10×2.8)/5
OB=2×2.8
OB=5.6cm
Then, consider OA/OC=AB/CD
10/5=6.5/CD
CD=(6.5×5)/10
CD=32.5/10
CD=3.25cm
(iii) We have to find the ratio of areas of △OAB and △OCD.
From (i) we proved that, △OAB∼△OCD
Then, area of (△OAB)/area of △OCD
AB2/CD2=(6.5)2/(3.25)2
=(6.5×6.5)/(3.25×3.25)
=2×2/1
=4/1
Therefore, the ratio of areas of △OAB and △OCD=4:1.