The best way to solve the question of triangles form exercise 6.3 of class 10th math, how i solve in easy way In the figure, ΔODC ∝ ¼ ΔOBA, ∠ BOC = 125° and ∠ CDO = 70°. Find ∠ DOC, ∠ DCO and ∠ OAB.
AnilSinghBoraGuru
In the figure, ΔODC ∝ ¼ ΔOBA, ∠ BOC = 125° and ∠ CDO = 70°. Find ∠ DOC, ∠ DCO and ∠ OAB. Q.2
Share



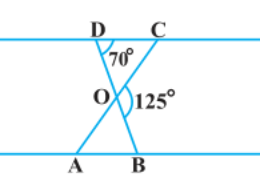

As we can see from the figure, DOB is a straight line.
Therefore, ∠DOC + ∠ COB = 180°
⇒ ∠DOC = 180° – 125° (Given, ∠ BOC = 125°)
= 55°
In ΔDOC, sum of the measures of the angles of a triangle is 180º
Therefore, ∠DCO + ∠ CDO + ∠ DOC = 180°
⇒ ∠DCO + 70º + 55º = 180°(Given, ∠ CDO = 70°)
⇒ ∠DCO = 55°
It is given that, ΔODC ∝ ¼ ΔOBA,
Therefore, ΔODC ~ ΔOBA.
Hence, Corresponding angles are equal in similar triangles
∠OAB = ∠OCD
⇒ ∠ OAB = 55°
∠OAB = ∠OCD
⇒ ∠OAB = 55°