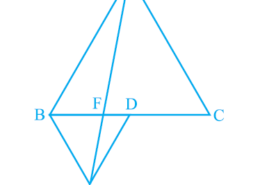
How i solve the question of class 9th ncert math of Areas of Parallelograms and Triangles chapter of exercise 9.4 of question no 5(1). I think it is very important question of class 9th give me the tricky way for solving this question In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:(i) ar (BDE) =1/4 ar (ABC)
AnilSinghBoraGuru
In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:(i) ar (BDE) =1/4 ar (ABC) Q.5 (1)
Share




Assume that G and H are the mid-points of the sides AB and AC respectively.
Join the mid-points with line-segment GH. Here, GH is parallel to third side.
, BC will be half of the length of BC by mid-point theorem.
∴ GH =1/2 BC and GH || BD
∴ GH = BD = DC and GH || BD (Since, D is the mid-point of BC)
Similarly,
GD = HC = HA
HD = AG = BG
, ΔABC is divided into 4 equal equilateral triangles ΔBGD, ΔAGH, ΔDHC and ΔGHD
We can say that,
ΔBGD = ¼ ΔABC
Considering, ΔBDG and ΔBDE
BD = BD (Common base)
Since both triangles are equilateral triangle, we can say that,
BG = BE
DG = DE
, ΔBDG ΔBDE [By SSS congruency]
, area (ΔBDG) = area (ΔBDE)
ar (ΔBDE) = ¼ ar (ΔABC)
Hence proved