Sir please help me for solving this question of class 10th of ncert book of math of circles chapter and exercise 10.2, give me the best and easy way to solve this problem In Fig. 10.13, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°.
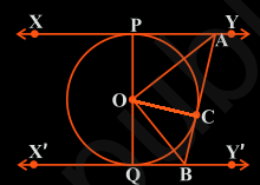
From the figure given in the textbook, join OC. Now, the diagram will be as-
Now the triangles △OPA and △OCA are similar using SSS congruency as:
(i) OP = OC They are the radii of the same circle
(ii) AO = AO It is the common side
(iii) AP = AC These are the tangents from point A
So, △OPA ≅ △OCA
Similarly,
△OQB ≅ △OCB
So,
∠POA = ∠COA … (Equation i)
And, ∠QOB = ∠COB … (Equation ii)
Since the line POQ is a straight line, it can be considered as a diameter of the circle.
So, ∠POA +∠COA +∠COB +∠QOB = 180°
Now, from equations (i) and equation (ii) we get,
2∠COA+2∠COB = 180°
∠COA+∠COB = 90°
∴∠AOB = 90°