Give me the best solution of question no.2 of class 10th math of exercise 10.2 of math, how i solve this question of circles chapter in easy and simple way give me the best way to solve this problem In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to (A) 60° (B) 70° (C) 80° (D) 90°
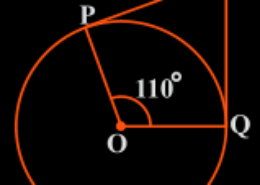
From the question, it is clear that OP is the radius of the circle to the tangent PT and OQ is the radius to the tangents TQ.
So, OP ⊥ PT and TQ ⊥ OQ
∴∠OPT = ∠OQT = 90°
Now, in the quadrilateral POQT, we know that the sum of the interior angles is 360°
So, ∠PTQ+∠POQ+∠OPT+∠OQT = 360°
Now, by putting the respective values we get,
∠PTQ +90°+110°+90° = 360°
∠PTQ = 70°
So, ∠PTQ is 70° which is option B